كيفية العثور على الارتفاع في مثلث متساوي الساقين؟ صيغة الاكتشاف ، خصائص الارتفاع في مثلث متساوي الساقين

الهندسة ليست مجرد كائن في المدرسة ،الذي يحتاج للحصول على تقييم ممتاز. هو أيضا المعرفة التي غالبا ما تكون مطلوبة في الحياة. على سبيل المثال ، عند بناء منزل بسقف مرتفع ، تحتاج إلى حساب سمك السجلات وعددها. هذا أمر سهل إذا كنت تعرف كيفية العثور على الارتفاع في مثلث متساوي الساقين. تعتمد البنى المعمارية على معرفة خصائص الأشكال الهندسية. أشكال المباني غالبا ما تشبه بصريا. الأهرامات المصرية ، والحزم مع الحليب والتطريز الفني واللوحات الشمالية وحتى الفطائر كلها مثلثات تحيط بشخص. وكما قال أفلاطون ، فإن العالم كله يقوم على مثلثات.

مثلث متساوي الساقين

لتوضيح ذلك ، ما سيتم مناقشته بعد ذلك ، يجدر تذكر أساسيات الهندسة.

المثلث هو متساوي الساقين إذا كان له جانبان متساوان. وتسمى دائما جانبي. الجانب ، أحجامها التي تختلف ، كانت تسمى الأرض.

المفاهيم الأساسية

مثل أي علم ، الهندسة له قواعده ومفاهيمه الأساسية الخاصة. هناك الكثير منهم. النظر فقط في تلك التي بدونها سيكون موضوعنا غير مفهوم إلى حد ما.

ارتفاع - وهذا هو خط مستقيم يرسم عمودي على الجانب المقابل.

الوسيط هو جزء موجه من أي رأس للمثلث حصريًا إلى منتصف الجانب المقابل.

زاوية المنصف هي شعاع يقسم الزاوية إلى نصفين.

إن النقطة الأساسية للمثلث هي خط مستقيم ، أو بالأحرى ، جزء من النقطة المندمجة للركن الذي يربط الرأس إلى الجانب الآخر.

من المهم جدا أن نتذكر أن الزاوية المنفردة هي بالضرورة شعاع ، ويكون المنصف للمثلث جزءًا من هذا الشعاع.

الزوايا في القاعدة

تقول النظرية أن الزوايا الموجودة فيأساس أي المثلث متساوي الساقين ، هي دائما متساوية. من السهل جداً إثبات هذه النظرية. النظر في المثلث متساوي الساقين ABC المبين ، والتي AB = BC. من الزاوية ABC ، ​​من الضروري رسم نصف موزع VD. الآن النظر في المثلثين التي تم الحصول عليها. وبحسب الحالة AB = BC ، يكون جانب AP بالنسبة للمثلثات شائعًا ، وتكون زوايا ABD و SVD متساوية ، لأن VD هو العامل المنصف. وبالإشارة إلى العلامة الأولى للمساواة ، يمكننا أن نستنتج بأمان أن المثلثات قيد النظر متساوية. وبالتالي ، فإن جميع الزوايا المقابلة متساوية. وبطبيعة الحال ، فإن الأطراف ، ولكن عند هذه النقطة سوف نعود في وقت لاحق.

ارتفاع مثلث متساوي الساقين

المبرهنة الرئيسية التي يستند إليها الحلتقريبا كل المشاكل ، أصوات مثل هذا: الارتفاع في مثلث متساوي الساقين هو منصفة ووسيط. لفهم معناها العملي (أو الجوهر) ، من الضروري تقديم بدل مساعد. لهذا من الضروري قطع مثلث متساوي الساقين من الورق. أسهل طريقة للقيام بذلك هي من ورقة tetrad القياسية في الخلية.

أضعاف المثلث الناتج في النصف ، محاذاةالجوانب الجانبية. ماذا حدث؟ مثلثان متساويان. الآن تحتاج إلى التحقق من التخمين. تتكشف اوريغامي. ارسم خطًا. باستخدام المنقلة ، تحقق من الزاوية بين الخط المسحوب وقاعدة المثلث. ماذا تقول زاوية 90 درجة؟ حقيقة أن الخط المرسوم هو عمودي. بحكم التعريف - الارتفاع. كيفية العثور على الارتفاع في مثلث متساوي الساقين ، قمنا بتصنيفه. الآن دعونا نتعامل مع الزوايا في الأعلى. باستخدام نفس المنقلة ، تحقق من الزوايا التي تشكلت الآن من الارتفاع. هم متساوون. هذا يعني أن الارتفاع هو أيضًا عامل أساسي. مسلّحًا بمسطرة ، قم بقياس الأطوال التي ينكسر فيها ارتفاع القاعدة. هم متساوون. وبالتالي ، فإن الارتفاع في مثلث متساوي الساقين يقسم القاعدة إلى نصفين وهو متوسط.

إثبات للنظرية

تبرهن المعونة البصرية بوضوح على صحة النظرية. لكن الهندسة - علم دقيق تمامًا ، لذلك يتطلب إثباتًا.

خلال النظر في المساواة من الزوايا معثبت المساواة من المثلثات. أذكر أن VD هو منصف ، ومثلثات AVD و SVD متساوية. وكان الاستنتاج هو: الجوانب المقابلة للمثلث ، وبطبيعة الحال ، فإن الزوايا متساوية. وبالتالي ، م = SD. لذلك ، VD هو الوسيط. يبقى أن تثبت أن VD هو الارتفاع. انطلاقا من المساواة بين المثلثات قيد النظر ، تبين أن زاوية ADB تساوي زاوية VDV. لكن هاتين الزاويتين متجاورتان ، وكما هو معروف ، يعطيان ما مجموعه 180 درجة. لذلك ، ما هي تساوي؟ بالطبع ، 90 درجة. وبالتالي ، VD هو الارتفاع في مثلث متساوي الساقين مرسوم إلى القاعدة. كما هو مطلوب لإثبات.

الميزات الرئيسية

• لحل المشاكل بنجاح ، من الضروري تذكر السمات الأساسية لمثلثات متساوي الساقين. يبدو أنها معكوسة للنظريات.
• إذا تم العثور على مساواة زاويتين في سياق حل مشكلة ، فإنك تتعامل مع مثلث متساوي الساقين.
• إذا كان من الممكن إثبات أن المتوسط ​​هو في نفس الوقت ارتفاع المثلث ، استنتج بجرأة - المثلث هو متساوي الساقين.
• إذا كان المنصف هو أيضًا الارتفاع ، فعندئذ استنادًا إلى الميزات الرئيسية ، يشار إلى المثلث باسم متساوي الساقين.
• وبالطبع ، إذا ظهر الوسيط في دور الارتفاع ، فإن مثلثًا من هذا القبيل هو متساوي الساقين.

صيغة الطول 1

ومع ذلك ، بالنسبة لمعظم المشكلات ، يجب البحث عن الارتفاع الحسابي. هذا هو السبب في أننا ننظر في كيفية العثور على الارتفاع في مثلث متساوي الساقين.

دعونا نعود إلى الشكل ABC الموضح أعلاه ، والذي فيه الجانبين ، و c هي القاعدة. VD هو ارتفاع هذا المثلث ، وله تسمية h.

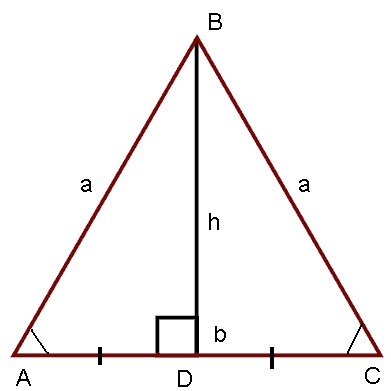
ما هو المثلث درهم؟ بما أن VD هي الارتفاع ، فإن مثلث الـ ABD مستطيل الشكل ، يمكن العثور على cathet منه. باستخدام معادلة فيثاغورس ، نحصل على:

AV² = АД² + ВД²

بعد أن حددنا من التعبير VD واستبدلنا بالتدوين المستخدم سابقا ، نحصل على:

Н² = ²² (в / 2) ².

من الضروري استخراج الجذر:

H = √²² - in² / 4.

إذا أزلنا من علامة الجذر then ، فستبدو الصيغة كما يلي:

H = ½ √4a² - in².

هذا هو الارتفاع في مثلث متساوي الساقين. يتبع الصيغة من نظرية فيثاغورس. حتى إذا نسيت هذا الإدخال الرمزي ، فعند معرفة طريقة البحث ، يمكنك دائمًا سحبها.

صيغة الطول 2

الصيغة الموضحة أعلاه هي الطريقة الرئيسية وفي أغلب الأحيانيتم استخدامه لحل معظم المشاكل الهندسية. لكنها ليست الوحيدة. في بعض الأحيان في الحالة ، بدلاً من القاعدة ، يتم إعطاء قيمة الزاوية. مع هذه البيانات ، وكيفية العثور على الارتفاع في مثلث متساوي الساقين؟ لحل مشاكل مماثلة ، من المستحسن استخدام صيغة مختلفة:

H = a / sin α ،

حيث H هو الارتفاع الموجه للقاعدة ،

لكن - الجانب ،

α هي الزاوية في القاعدة.

إذا كانت المهمة تعطي قيمة الزاوية في القمة ، فإن الارتفاع في مثلث متساوي الساقين يكون على النحو التالي:

H = a / cos (β / 2) ،

حيث H هو الارتفاع الذي انخفض على القاعدة ،

β هي الزاوية في القمة ،

هو الجانب.

مثلث مستطيل متساوي الساقين

خاصية مثيرة جدا للاهتمام هي المثلث ، الذي تبلغ ذروته 90 درجة. النظر في المثلث الصحيح ABC. كما في الحالات السابقة ، يكون VD هو الارتفاع الموجه للقاعدة.

الزوايا في القاعدة متساوية. احسب عملهم العظيم لن يكون:

α = (180-90) / 2.

وبالتالي ، الزوايا في القاعدة ،دائما 45 درجة. الآن النظر في مثلث ADV. إنه مستطيل أيضًا. دعونا نجد زاوية عبد. من خلال الحسابات البسيطة ، نحصل على 45 درجة. وبالتالي ، فإن هذا المثلث ليس مستطيلاً فقط ، ولكن أيضًا متساوي الساقين. الطرفان AD و VD هما وجهان جانبيان ومتساوون فيما بينهما.

لكن الجانب BP في نفس الوقت نصفجانب التيار المتردد. وتبين أن الارتفاع في مثلث متساوي الساقين هو نصف القاعدة ، وإذا تم كتابته في صيغة صيغة ، نحصل على التعبير التالي:

ع = ب / 2.

يجب أن نتذكر أن هذه الصيغة هي حالة خاصة حصرية ، ويمكن استخدامها فقط لمثلثات متساوي الساقين مستطيلة الشكل.

مثلثات ذهبية

المثير جدا للاهتمام هو المثلث الذهبي. في هذا الشكل ، تساوي نسبة الطرف إلى القاعدة القيمة المسماة رقم Phidias. الزاوية في الأعلى 36 درجة ، في القاعدة - 72 درجة. وقد أعجب هذا المثلث من قبل فيثاغورس. مبادئ المثلث الذهبي هي أساس العديد من الروائع الخالدة. بنيت على جميع النجوم الخماسية على تقاطع مثلثات متساوي الساقين. بالنسبة للعديد من الإبداعات ، استخدم ليوناردو دافنشي مبدأ "المثلث الذهبي". ويستند تكوين "Gioconda" على وجه التحديد على الأرقام التي تخلق البنتاغون نجم منتظم.

لوحة "التكعيبية"، واحدة من أعمال بابلو بيكاسو، المنظر الخلاب يشكل أساس مثلث متساوي الساقين.