استنتاجات ديراك. معادلة ديراك. نظرية المجال الكمي

هذه المقالة مكرسة لعمل بول ديراك ،المعادلة التي أثرت إلى حد كبير ميكانيكا الكم. فهو يصف المفاهيم الأساسية اللازمة لفهم المعنى الفيزيائي للمعادلة ، بالإضافة إلى طرق استخدامها.

العلم والعلماء

الشخص الذي لا يرتبط بالعلوم ، يمثلعملية التعدين المعرفة ببعض العمل السحري. والعلماء ، في رأي هؤلاء الناس ، هم الذين يتكلمون بلغة غير مفهومة وهم متكبرون بعض الشيء. بالتعرّف على الباحث ، يقول شخص بعيد عن العلم على الفور إنه لا يفهم الفيزياء في المدرسة. وهكذا ، يبتز الفلسطينيون من المعرفة العلمية ويطلب من محاور أكثر تعليما أن يتكلموا بشكل أسهل وأكثر وضوحا. بالتأكيد ، تم الترحيب بول ديراك ، الذي نعتبره معادلة ، بنفس الطريقة.

الجسيمات الأولية

لطالما كان هيكل المادة يثير الفضولالعقول. في اليونان القديمة ، لاحظ الناس أن الخطوات الرخامية ، التي انقلبت عليها أرجل كثيرة ، تغيرت في النهاية ، واقترح أن كل قدم أو صندل يحمل جزيءًا صغيرًا من المادة. هذه العناصر قررت أن تسمى "ذرات" أي "غير قابلة للتجزئة". يبقى الاسم ، ولكن اتضح أن كلا من الذرات والجسيمات التي تشكل الذرات هي أيضا معقدة ، معقدة. تسمى هذه الجسيمات بجسيمات أولية. ويخصص عمل ديراك لهم ، معادلة لا تسمح فقط لشرح دوران الإلكترون ، ولكن أيضا لتحمل وجود مضاد للإلكترون.

موجة الجوف المزدوج

تطوير التصوير الفوتوغرافي في النهايةلم يستلزم القرن التاسع عشر مجرد طريقة لالتقاط صورهم وأطعمهم وقططهم فحسب ، بل شمل كذلك إمكانات العلم. بعد أن تلقى مثل هذه الأداة المريحة كصورة سريعة (استدعي ، قبل أن يستمر التعريض إلى 30-40 دقيقة) ، بدأ العلماء بتسجيل مجموعة متنوعة من الأطياف بكثافة.

النظريات الموجودة للهيكلالمواد لا يمكن أن تفسر أو تتنبأ بشكل فريد بأطياف الجزيئات المعقدة. أولا، أظهرت التجربة الشهيرة روثرفورد أن الذرة لا تتجزأ ذلك: كان قلبه نواة إيجابية الثقيلة حولها إلكترونات سالبة تقدم سهلة. ثم أثبت اكتشاف النشاط الإشعاعي أن النواة ليست متراصة، وتتكون من البروتونات والنيوترونات. ومن ثم اكتشاف في وقت واحد تقريبا من الكم من الطاقة، ومبدأ الارتياب لهايزنبرج والطبيعة الاحتمالية للجسيمات الأولية موقع تعطي زخما لتطوير نهج علمي جديد تماما لدراسة العالم المحيط. كان هناك قسم جديد - فيزياء الجسيمات الأولية.

كانت القضية الرئيسية في فجر هذا القرن من اكتشافات كبيرة في نطاق صغير للغاية هو تفسير وجود الجسيمات الأولية وكتلة وخصائص الموجة.

أثبت أينشتاين أنه حتى فوتون فوتغرافيلديه كتلة ، لأنه ينقل دفعة إلى جسم صلب ، والذي يسقط (ظاهرة ضغط الضوء). في هذه الحالة ، تحدثت العديد من التجارب على تشتت الإلكترونات على الشقوق على الأقل عن وجود الحيود والتداخل فيها ، وهذا أمر غريب فقط للموجة. ونتيجة لذلك ، كان علي أن أعترف: الجسيمات الأولية هي كائن ذو كتلة وموجة. وهذا يعني أن كتلة الإلكترون ، كما يقول ، "لطخت" إلى حزمة طاقة ذات خصائص موجية. هذا المبدأ من ثنائية الموجة الجسيمية جعل من الممكن أن نفهم أولاً لماذا لا يقع الإلكترون على النواة ، ولأي أسباب هناك مدارات في الذرة ، وتكون الانتقالات بينهما فجائية. هذه التحولات تولد طيفًا فريدًا لأي مادة. علاوة على ذلك ، يجب أن تشرح فيزياء الجسيمات الأولية خصائص الجسيمات نفسها ، بالإضافة إلى تفاعلها.

وظيفة الموجة والأعداد الكمية

لقد قام إيروين شرودنغر بعمل رائع حتى الآن(اكتشاف غير مكتمل على أساسه في وقت لاحق ، بنى بول ديراك نظريته). لقد أثبت أن حالة أي جسيم أولي ، على سبيل المثال ، من الإلكترون ، وصفت من قبل الدالة الموجة ψ. هذا لا يعني أي شيء في حد ذاته ، ولكن ساحةه ستظهر احتمالية العثور على إلكترون في مكان معين في الفضاء. يتم وصف حالة الجسيم الأولي في الذرة (أو أي نظام آخر) بأربعة أرقام كمومية. هذا هو الرئيسي (n) ، المداري (l) ، المغناطيسي (m) و spin (م_الصورة) من الرقم. أنها تظهر خصائص الجسيمات الأولية. كقياس ، يمكنك إحضار شريط من النفط. خصائصه - الوزن والحجم واللون والدهون. ومع ذلك ، لا يمكن فهم الخصائص التي تصف الجسيمات الأولية بشكل حدسي ، يجب أن تتحقق من خلال الوصف الرياضي. عمل ديراك ، معادلاته هي محور هذه المقالة ، مكرس للرقم الأخير.

غزل

قبل الشروع مباشرة في المعادلة ، من الضروري توضيح ماهية رقم الدوران m_الصورة. إنها تُظهر اللحظة الجوهرية لعزم الإلكترون والجسيمات الأولية الأخرى. يكون هذا الرقم موجبًا دائمًا ويمكن أن يأخذ قيمة صحيحة أو قيمة صفرية أو نصف صحيحة (للإلكترون m_الصورة = 1/2). تدور هي قيمة ناقلات والوحيد الذي يصف اتجاه الإلكترون. تضع نظرية المجال الكمي الدوران على أساس تفاعل التبادل ، الذي لا يوجد تناظري في ميكانيكا بديهية عادة. يوضح رقم الدوران كيف يجب أن يتحول الموجه إلى الحالة الأصلية. مثال على ذلك هو قلم كرة نقطة عادي (جزء الكتابة هو اتجاه موجب للمتجه). لجعلها تأتي إلى حالتها الأصلية ، يجب أن تدور 360 درجة. هذا الموقف يتوافق مع دوران يساوي 1. من أجل دوران 1/2 ، مثل الإلكترون ، يجب أن يكون الدوران 720 درجة. لذا ، بالإضافة إلى الغرائز الرياضية ، يجب على المرء تطوير التفكير المكاني من أجل فهم هذه الخاصية. أكثر من ذلك بقليل تحدثنا عن وظيفة الموجة. إنه "الممثل" الرئيسي لمعادلة شرودنغر ، الذي يصف حالة وموضع جسيم أولي. لكن هذه العلاقة في شكلها الأصلي مخصصة للجسيمات بدون دوران. لا يمكننا وصف حالة الإلكترون إلا إذا قمنا بتعميم معادلة شرودنغر ، التي تمت في عمل ديراك.

البوسون والفرميونات

Fermion هو جسيم ذو قيمة دوران نصف متكاملة. يتم ترتيب الفرميونات في الأنظمة (مثل ذرات) وفقا لمبدأ استبعاد باولي: في كل دولة يجب أن يكون هناك أكثر من واحد الجسيمات. وهكذا، كل إلكترون في الذرة يختلف بعض الشيء عن الآخرين (بعض عدد الكم له معنى مختلف). نظرية المجال الكم يصف حالة أخرى - البوزونات. لديهم زيادة ونقصان، ويمكن للجميع أن تكون في وقت واحد في دولة واحدة. تنفيذ هذه الحالة تسمى بوز-آينشتاين. وعلى الرغم من إلى حد ما أكدت أيضا إمكانية النظرية للحصول عليه، ويتم ذلك أساسا في عام 1995 وحده.

معادلة ديراك

كما ذكرنا أعلاه ، استنتج بول ديراكمعادلة المجال الكلاسيكي للإلكترون. كما يصف حالات الفيرميونات الأخرى. المعنى المادي للعلاقة معقد ومتعدد الأوجه ، والعديد من الاستنتاجات الأساسية تتبع من شكلها. شكل المعادلة هو:

- (مولودية² α₀+ c Σ a_كص_ك {k = 0-3}) ψ (x، t) = i ħ {∂ ψ / ∂ t (x، t)}،

حيث م - كتلة فرميون (خاصة الإلكترون) ، مع - سرعة الضوء ، ص_ك- ثلاثة عوامل لمكونات الزخم (على طول المحاور x ، y ، z) ، ħ هي ثابت بلانك المقتطع ، و x و t ثلاثة إحداثيات مكانية (تتوافق مع المحاور X ، Y ، Z) والوقت ، على التوالي ، و ψ(x، t) عبارة عن دالة موجة معقدة رباعية العناصر ، α_ك (ك = 0 ، 1 ، 2 ، 3) هي مصفوفات باولي. هذا الأخير هو المشغلين الخطيين الذين يعملون على وظيفة الموجة ومساحتها. هذه الصيغة معقدة إلى حد ما. لفهم حتى مكوناته ، يجب علينا فهم التعريفات الأساسية لميكانيكا الكم. أيضا ، ينبغي للمرء أن يكون لديه معرفة رياضية رائعة ، على الأقل لمعرفة ما هي ناقلات ، مصفوفة والمشغل. شكل المعادلة سوف يخبر الخبير أكثر من مكوناته. الشخص الذي يتقن الفيزياء النووية والمعروف بميكانيكا الكم سوف يفهم أهمية هذه العلاقة. ومع ذلك ، يجب أن نعترف بأن معادلات ديراك وشرودنغر هي مجرد أسس أولية للوصف الرياضي للعمليات التي تحدث في عالم الكميات الكمومية. يجب أن يفهم علماء الفيزياء النظرية الذين قرروا تكريس أنفسهم للجسيمات الأولية وتفاعلهم جوهر هذه العلاقات في السنة الثانية من المعهد. لكن هذا العلم رائع ، وفي هذا المجال يمكنك تحقيق اختراق أو تخليد اسمك ، أو تخصيص معادلته أو تحوله أو ملكيته.

المعنى المادي للمعادلة

كما وعدنا ، فإننا نقول ما هي الاستنتاجات المخفيةمعادلة ديراك للإلكترون. أولا ، من هذه العلاقة يصبح من الواضح أن دوران الإلكترون هو ½. وثانيا ، وفقا للمعادلة ، فإن الإلكترون له عزم مغناطيسي خاص به. وهي تساوي مغنطيس بوهر (وحدة العزم المغناطيسي الأولي). ولكن أهم نتيجة للحصول على هذه العلاقة تكمن في عامل α غير محسوس_ك. اشتقاق معادلة ديراك من معادلة شرودنغراستغرق وقتا طويلا. في البداية اعتقد Dirac أن هؤلاء المشغلين تتداخل مع النسبة. باستخدام الحيل الرياضية المختلفة ، حاول استبعادهم من المعادلة ، لكنه لم ينجح. ونتيجة لذلك ، تحتوي معادلة ديراك على جسيم حر على أربعة عوامل α. كل واحد منهم عبارة عن مصفوفة [4x4]. اثنين تتوافق مع الكتلة الإيجابية للإلكترون ، مما يثبت وجود موقفين من دورانه. يعطي الاثنان الآخرون حلاً للكتلة السالبة للجسيم. إن أبسط المعارف في الفيزياء يمنح الإنسان الفرصة لاستنتاج أن هذا مستحيل في الواقع. ولكن نتيجة للتجربة ، تبين أن المصفوفتين الأخيرتين تمثلان حلولًا للجسيم الموجود المقابل للإلكترون ، وهو الإلكترون المضاد. مثل الإلكترون ، فإن البوزيترون (كما يطلق عليه هذا الجسيم) له كتلة ، لكن شحنته إيجابية.

بوزيترون

كما كان الحال في كثير من الأحيان في عصر اكتشاف الكم ، ديراكفي البداية لم يصدق استنتاجه الخاص. لم يجرؤ على نشر تنبؤات جسيم جديد بشكل علني. صحيح ، في مجموعة متنوعة من المقالات وفي مختلف الندوات ، أكد العالم على إمكانية وجودها ، على الرغم من أنه لم يفترضها. ولكن بعد فترة وجيزة من اشتقاق هذه العلاقة الشهيرة ، تم العثور على بوزيترون في الإشعاع الكوني. وبالتالي ، تم تأكيد وجودها تجريبيا. البوزيترون هو العنصر الأول في المادة المضادة التي يكتشفها البشر. يولد البوزيترون كواحد من الزوجين التوأم (توأم آخر هو إلكترون) عندما تتفاعل فوتونات طاقة عالية للغاية مع نوى المادة في حقل كهربائي قوي. لن نقتبس الأرقام (القارئ المهتم سيجد كل المعلومات الضرورية بنفسه). ومع ذلك ، ينبغي التأكيد على أننا نتحدث عن المقاييس الفضائية. فقط انفجارات المستعرات العظمى وتصادمات المجرات قادرة على إنتاج الفوتونات من الطاقة اللازمة. يتم احتواؤها أيضا في كمية معينة في نوى النجوم الساخنة ، بما في ذلك الشمس. لكن الرجل يسعى دائما لمصلحته الخاصة. إبادة المادة مع المادة المضادة يعطي الكثير من الطاقة. للحد من هذه العملية والبدء في ذلك لصالح البشرية (على سبيل المثال ، فإن محركات البطانات بين النجوم على الفناء ستكون فعالة) ، وتعلم الناس كيفية صنع البروتونات في المختبر.

على وجه الخصوص ، مسرعات كبيرة (مثل hadronicالمصادم) يمكن أن تخلق أزواج الإلكترون-البوزيترون. في السابق ، كان هناك اقتراح أيضًا بعدم وجود جسيمات أولية فقط (هناك العديد من الأضداد إلى جانب الإلكترون) ، ولكن أيضًا مضاد المادة بأكمله. حتى قطعة صغيرة جدا من أي مادة كيميائية من المادة المضادة ستوفر الطاقة لكامل الكوكب (ربما كان كريبتونيت الخارق هو مضاد المادة؟).

لكن للأسف ، فإن خلق المادة المضادة أثقل من النواةلم يوثق الهيدروجين في الكون المنظور. ومع ذلك ، إذا كان القارئ يعتقد أن تفاعل المادة (نشدد عليه ، فهو المادة ، وليس الإلكترون الفردي) مع البوزيترون ينتهي على الفور بالإبادة ، فإنه مخطئ. عندما يتم تباطؤ البوزيترون بسرعة عالية ، يظهر زوج من الإلكترونات-البوزيترون ، يسمى بوزيترونيوم ، في سوائل معينة مع احتمال غير صفري. هذا التكوين لديه بعض خصائص الذرة ويمكنه حتى الدخول في التفاعلات الكيميائية. لكن هذا الترادف الهش لا يدوم طويلاً ثم يهلك مع انبعاث اثنين ، وفي بعض الحالات ، ثلاثة كمات غاما.

عيوب المعادلة

على الرغم من حقيقة أنه بسبب هذه العلاقةتم الكشف عن مضاد الإلكترون ومضاد ، لديه عيب كبير. إن سجل المعادلة والنموذج المبني على أساسها غير قادر على التنبؤ بكيفية توليد الجسيمات وتدميرها. هذا نوع من السخرية للعالم الكمي: النظرية التي توقعت ولادة أزواج المادة - المادة المضادة - غير قادرة على وصف هذه العملية بشكل مناسب. تم القضاء على هذا النقص في نظرية المجال الكمي. من خلال إدخال تكمية الحقول ، يصف هذا النموذج تفاعلها ، بما في ذلك إنشاء وإزالة الجسيمات الأولية. من خلال "نظرية المجال الكمي" في هذه الحالة يعني مصطلح محدد تماما. هذا مجال فيزياء يدرس سلوك الحقول الكمية.

معادلة ديراك بإحداثيات أسطوانية

أولا ، دعنا نقول ما هو أسطوانينظام الإحداثيات. بدلاً من المحاور الثلاثة المتعامدة المتعاقبة المعتادة ، يتم استخدام الزاوية ونصف القطر والارتفاع لتحديد الموقع الدقيق لنقطة في الفضاء. هذا هو نفس نظام الإحداثيات القطبية على المستوى ، فقط البعد الثالث - يضاف الارتفاع. هذا النظام مناسب إذا كان مطلوبًا أن يصف أو يحقق سطحًا متماثلًا فيما يتعلق بأحد المحاور. بالنسبة لميكانيكا الكم ، تعتبر هذه أداة مفيدة جدًا ومفيدة تسمح لك بتقليل حجم الصيغ وعدد الحسابات بشكل ملحوظ. هذا هو نتيجة لمحاذاة سحابة الإلكترون في الذرة. يتم حل معادلة ديراك في إحداثيات أسطوانية بشكل مختلف نوعًا ما عن النظام المعتاد ، وفي بعض الأحيان تعطي نتائج غير متوقعة. على سبيل المثال ، تم حل بعض المشاكل التطبيقية لتحديد سلوك الجسيمات الأولية (غالباً الإلكترونات) في حقل كمي عن طريق تحويل شكل المعادلة إلى إحداثيات أسطوانية.

استخدام المعادلة لتحديد هيكل الجزيئات

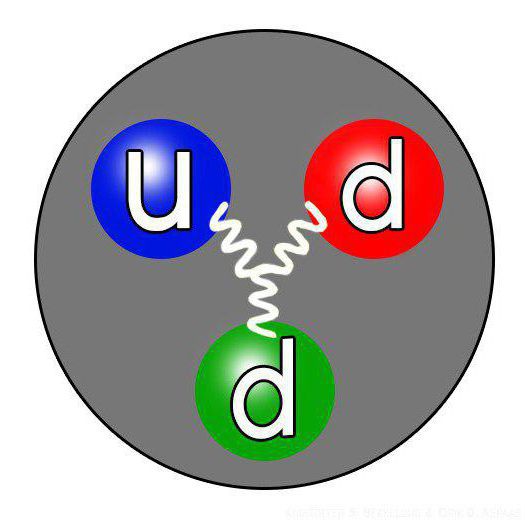
تصف هذه المعادلة جسيمات بسيطة: تلك التي لا تتكون من عناصر أصغر. العلم الحديث قادر على قياس اللحظات المغناطيسية بدقة عالية بما فيه الكفاية. وهكذا ، فإن التباين بين القيمة المحسوبة بواسطة معادلة ديراك والعزم المغناطيسي المقاس تجريبيا سوف يشير بشكل غير مباشر إلى بنية معقدة من الجسيم. نذكر أن هذه المعادلة تنطبق على الفرميونات ، وتدورها هي نصف متكاملة. باستخدام هذه المعادلة ، تم تأكيد البنية المعقدة لل protروتونات والنيوترونات. كل واحد منهم يتكون من عناصر أصغر ، تسمى الكواركات. يحافظ حقل gluon على الكواركات معًا ، ولا يسمح لها بالانهيار. هناك نظرية أن الكواركات ليست الجسيمات الأكثر أهمية في عالمنا. ولكن في حين أن الناس ليس لديهم ما يكفي من القوة التقنية لفحص ذلك.