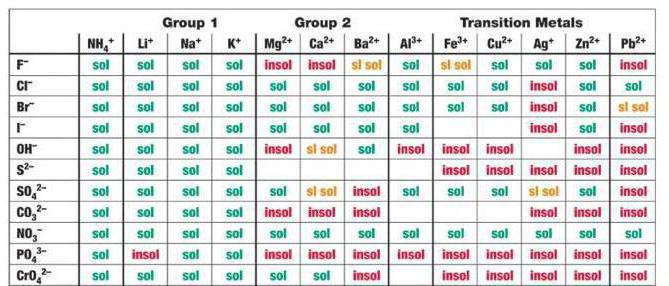
هل نسيت كيف تحل المعادلة التربيعية غير المكتملة؟

كيفية حل معادلة من الدرجة الثانية غير مكتملة؟ من المعروف أنه متغير معين لفأس المساواة²+ bx + c = a ، حيث تكون a و b و c حقيقيةمعاملات غير معروفة x ، وحيث a، a ، و b و c أصفار-بشكل متزامن أو منفصل. على سبيل المثال ، c = o ، in ≠ o أو العكس. تذكرنا تقريبًا تعريف المعادلة التربيعية.

سنوضح

و trinomial من الدرجة الثانية يساوي الصفر. يمكن لمعاملها الأول a، o و b و c أن تأخذ أي قيم. ستكون قيمة المتغير x جذر المعادلة ، عند استبدالها ، ستعيده إلى المساواة العددية الصحيحة. دعونا نركز على الجذور الحقيقية ، على الرغم من أن حل المعادلة يمكن أن يكون عددًا معقدًا. من المعتاد استدعاء معادلة لا يساوي أي معاملات فيها a ، و o ، إلى o ، c ≠ o.
دعونا حل مثال. 2²-9x-5 = 0 ، نجد
D = 81 + 40 = 121 ،
D إيجابي ، ثم هناك جذور ، X₁ = (9 + √121): 4 = 5 ، والثاني x₂ = (9-√121): 4 = -o، 5. سيساعدك الفحص على التأكد من صحته.

هنا هو الحل خطوة بخطوة من المعادلة التربيعية

من خلال التمييز ، يمكن حل أي معادلة ، على الجانب الأيسر منها يوجد تكراري تربيعي معروف لـ ≠ o. في مثالنا. 2²-9x-5 = 0 (الفأس²+ вх + с = о)

• نجد أولا D التمييز من الصيغة المعروفة في²-4as.
• نتحقق من قيمة D: لدينا أكثر من صفر ، تساوي الصفر أو أقل.
• نحن نعلم أنه إذا كانت D> 0 ، فإن المعادلة التربيعية لها جذرين حقيقيين متميزيين فقط ، يشار إليهما بـ x₁ عادة س₂,
  إليك كيفية حساب:
  س₁ = (-B + √D): (2a) ، والثانية: x₂ = (-in-√D): (2a).
• D = o هو جذر واحد ، أو ، كما يقولون ، متساويين:
  س₁ تساوي x₂ ويساوي: (2 أ).
• وأخيرًا ، يعني D <o أن المعادلة ليس لها جذور حقيقية.

دعونا ننظر في ما هي معادلات غير كاملة من الدرجة الثانية

1. آه²+ ix = o. مصطلح مجاني ، معامل c لـ x⁰، هنا صفر ، في ≠ س.
   كيفية حل معادلة من الدرجة الثانية غير مكتملة من هذا النوع؟ نأخذ x للأقواس. نذكر عندما يكون ناتج عاملين هو صفر.
   x (ax + b) = o ، يمكن أن يكون هذا عند x = 0 أو عند ax + b = o.
   حل المعادلة الخطية الثانية ، لدينا x = -v / a.
   نتيجة لذلك ، لدينا جذور س₁ = 0 ، من خلال الحسابات س₂ = -b / a_.
2. الآن معامل x يساوي o ، و c لا تساوي (≠) o.
   س²+ c = o. نحن ننقل c من الجانب الأيمن للمساواة ، نحصل على x² = ج. هذه المعادلة لها جذور حقيقية فقط عندما يكون -c رقم موجب (c <o) ،
   س₁ ثم تساوي √ (-c) ، على الترتيب ، x₂ - -√ (-s). خلاف ذلك ، فإن المعادلة ليس لها جذور على الإطلاق.
3. الخيار الأخير: ب = ج = س ، وهذا هو ، آه² = س. وبطبيعة الحال ، فإن هذه المعادلة البسيطة لها جذر واحد ، x = o.

حالات خاصة

كيفية حل معادلة من الدرجة الثانية غير مكتملة ، والآن نحن نأخذ أي نوع.

• في المعادلة التربيعية الكاملة ، يكون المعامل الثاني لـ x عبارة عن رقم زوجي.
  دعونا ك = س ، 5 ب. لدينا صيغ لحساب التمييز والجذور.
  D / 4 = k²- ac ، وتحسب الجذور كما س_1,2 = (-k ± √ (D / 4)) / a لـ D> o.
  x = -k / a لـ D = o.
  لا توجد جذور ل D <o.
• هناك معادلات مربعة مخفضة ، عندما يكون معامل x في المربع 1 ، يتم كتابتها عادة x² + px + q = o. تنطبق جميع الصيغ أعلاه عليها ، ولكن الحسابات أبسط نوعًا ما.
  مثال ، س²-4x-9 = 0. نحسب D: 2²+9 ، D = 13.
  س₁ = 2 + √13، x₂ = 2-√13.
• وبالإضافة إلى ذلك، نظرا تطبيقها بسهولةنظرية فييت. تقول أن مجموع جذور المعادلة هو -p ، المعامل الثاني مع علامة الطرح (بمعنى الإشارة المعاكسة) ، وناتج هذه الجذور نفسها تساوي q ، المدى الحر. تحقق من مدى سهولة تحديد جذور هذه المعادلة شفهيًا. للحصول على قيمة غير مخفضة (لجميع المعاملات لا تساوي الصفر) هذه النظرية قابلة للتطبيق على النحو التالي: المبلغ x₁+ س₂ يساوي -a / a ، المنتج x₁X₂ يساوي c / a.

مجموع المدى المجاني c والمعامل الأول aيساوي المعامل b. في هذه الحالة ، تحتوي المعادلة على جذر واحد على الأقل (من السهل إثباته) ، ويجب أن يكون الأول هو -1 ، والثاني يجب أن يكون c / a ، إذا كان موجودًا. كيفية حل المعادلة التربيعية غير المكتملة ، يمكنك التحقق من نفسك. أبسط من البسيط. يمكن أن تكون المعاملات في بعض العلاقات فيما بينها

• س²+ x = o، 7x²-7 = س.
• مجموع كل المعاملات هو س.
  جذور هذه المعادلة هي 1 و c / a. مثال ، 2x²-15x + 13 = o.
  س₁ = 1 ، س₂ = 13/2.

هناك عدد من الطرق الأخرى لحل مختلفمعادلات الدرجة الثانية. هنا ، على سبيل المثال ، هي طريقة فصل مربع كامل من كثير الحدود. هناك عدة طرق بيانية. عندما تعالج في كثير من الأحيان مثل هذه الأمثلة ، ستتعلم كيفية "النقر" عليها مثل البذور ، لأن جميع الطرق تتبادر إلى الذهن تلقائيًا.