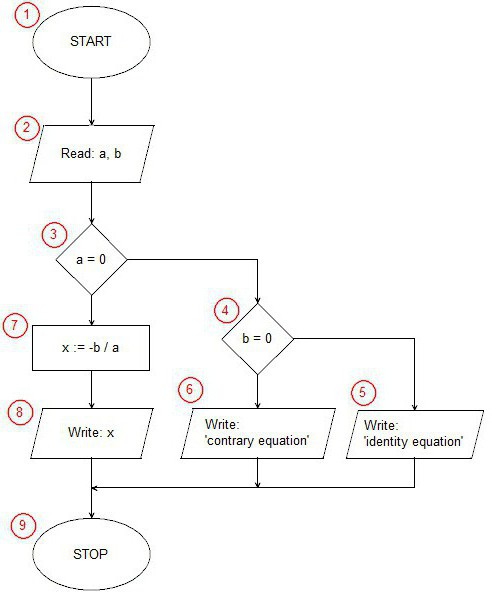
طريقة الاستيفاء الداخلي: الأنواع الأساسية والخوارزميات الحاسوبية
عدد كبير من المشاكل الرياضيةيرتبط مع وجود توزيع غير منتظم في مساحة المعلومات. نحن نتحدث عن أنظمة المعلومات جغرافياً ، لأنه يوجد فيها من الممكن قياس الكميات الضرورية في نقاط معينة. لحل هذه المشاكل ، غالباً ما يتم استخدام طريقة أو أكثر من الاستيفاء.
تعريف

الاستيفاء هو طريقة حسابالقيم المتوسطة للقيم من خلال مجموعة القيم المنفصلة المتاحة. الطرق الأكثر شيوعا للاستيفاء هي: طريقة المسافات الموزونة العكسية ، سطح الاتجاه والكينغ.
الأساليب الأساسية للاستيفاء
لذلك ، دعونا نلقي نظرة فاحصة على الطريقة الأولى ، وجوهرهاهو تأثير النقاط التي هي أقرب إلى النسبية تشير التقديرات إلى موقع أبعد من ذلك. مع ينطوي هذا الأسلوب الاستيفاء اختيار من التضاريس في حي معين من نقطة محددة، لها التأثير الأكبر على ذلك. وبالتالي اختيار الحد الأقصى نطاق البحث أو عدد من النقاط التي تقع على مقربة من نقطة معينة. ويرد مزيد من التعديل بالوزن في كل نقطة معينة، والذي يحسب وفقا للمسافة من نقطة معينة. وبهذه الطريقة فقط يمكن تحقيق ذلك من خلال مساهمة أكبر أقرب نقطة في ارتفاع محرف بالمقارنة مع نقاط بعيدة من المجموعة.
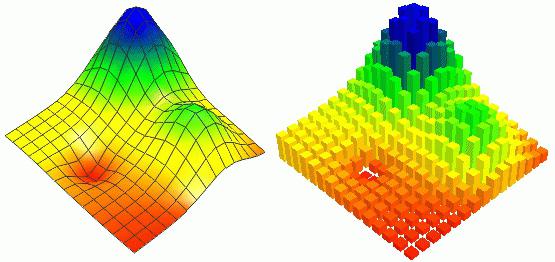

استخدام الاستيفاء التربيعي
هناك أداة أخرى لتحديدوالنقاط المحددة هي طريقة الاستكمال التربيعي ، الذي يتمثل جوهره في استبدال دالة ما على فاصل معين بفعل مكافئ تربيعي. في الوقت نفسه ، يقدر الحد الأقصى لها من الناحية التحليلية. بعد اكتشافه تقريبًا (الحد الأدنى أو الحد الأقصى) ، من الضروري تحديد نطاق معين من القيم ، وبعد ذلك البحث عن الحل للمتابعة. تكرار هذا الإجراء ، من الممكن ، باستخدام إجراء تكراري ، لتحسين قيمة هذه المعادلة للنتيجة مع الدقة المحددة في بيان المشكلة.