ما هو لا يتجزأ، وما هو معناها المادي
كان ظهور مفهوم التكامل جزءًا منضرورة البحث عن وظيفة مضادة للدواء فيما يتعلق بمشتقاتها ، وكذلك تحديد كمية العمل ، ومساحة الأشكال المعقدة ، والمسافة المقطوعة ، مع المعلمات المحددة بواسطة المنحنيات الموصوفة بواسطة صيغ غير خطية.
بالطبع
لكن القوة يمكن أن تتغير على مدار العمل ، وفي نوع ما من الاعتماد الطبيعي. وينشأ نفس الموقف مع حساب المسافة المقطوعة إذا لم تكن السرعة ثابتة.
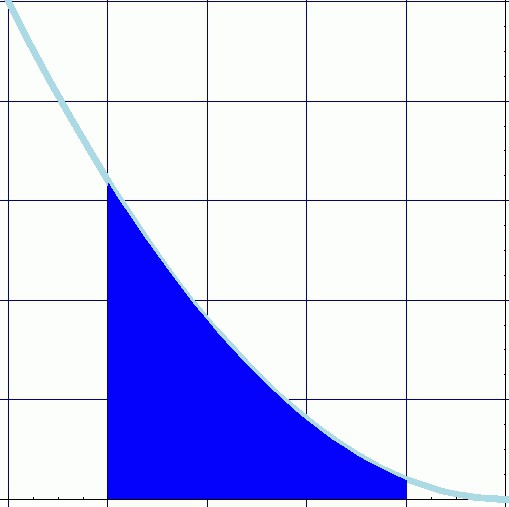
لذلك ، من الواضح ما هو جزء لا يتجزأ من. إن تحديده كمجموع لمنتجات قيم دالة بزيادات متناهية الصغر للحجة يصف تماما المعنى الرئيسي لهذا المفهوم كمنطقة الشكل المحدد من الأعلى بواسطة خط الوظيفة ، وعلى طول الحواف بحدود التعريف.
جان جاستون داربوكس ، عالم الرياضيات الفرنسي ، فيالنصف الثاني من القرن التاسع عشر شرح بوضوح ما هو التكامل. لقد فعل ذلك بكل وضوح أنه على العموم ، ليس من الصعب حتى لطالب في المدرسة الثانوية أن يفهم هذا السؤال.

افترض أن هناك وظيفة من أي شكل معقد. المحور الصادي، والتي تترسب قيمة حجة، وينقسم إلى فترات صغيرة، من الناحية المثالية، فهي صغيرة بشكل لا نهائي، ولكن لأن مفهوم اللانهاية مجردة تماما، ويكفي أن نتخيل مجرد قطعة صغيرة، والمبلغ الذي عادة ما يرمز له بالحرف اليوناني Δ (دلتا).
كانت الوظيفة "قطع" في الطوب الصغيرة.
لكل قيمة من الوسيطة هناك تتطابق مع نقطةمحور تنسيق الذي تودع القيم المناظرة وظيفة. ولكن كما الحدود في المنطقة المحددة اثنين، فإن القيم وظائف أيضا أن يكون اثنين أو أكثر وأقل.
مجموع منتجات القيم الكبيرة علىتسمى الزيادة the مبلغ Darboux الكبير ، ويتم تسميتها بـ S. تبعاً لذلك ، فإن القيم الأصغر على الجزء المحدد مضروبة بـ Δ جميعها تشكل مبلغًا صغيرًا من Darboux. يشبه القسم نفسه شبه منحرف مستطيل ، حيث يمكن إهمال انحناء خط الوظيفة بزيادة متناهية في الصغر. إن أبسط طريقة للعثور على مساحة مثل هذا الشكل الهندسي هو إضافة منتجات ذات قيمة أكبر وأصغر إلى زيادة and-and وزيادة القسمة على اثنين ، أي تعريفها كمتوسط حسابي.
هذا هو التكامل Darboux:
s = Σf (x) Δ هو مبلغ صغير ؛
S = Σf (x + Δ) Δ هو مبلغ كبير.
إذن ، ما هو التكامل؟ المنطقة التي يحدها خط الوظيفة وحدود التعريف ستكون:

∫f (x) dx = {(S + s) / 2} + c
أي أن المتوسط الحسابي لمجموعتي داربوكس الكبيرة والصغيرة هو قيمة ثابتة ، يتم إبطالها عن طريق التمييز.
انطلاقا من التعبير الهندسي لهذامفهوم ، يصبح المعنى المادي للكامل واضح. تكون مساحة الشكل ، التي تحددها وظيفة السرعة ، ويحدها الفاصل الزمني على امتداد abscissa ، هي طول المسار الذي تم اجتيازه.
L = ∫f (x) dx على الفاصل الزمني من t1 إلى t2 ،
حيث
f (x) هي دالة السرعة ، وهي الصيغة التي تتغير بها مع الزمن ؛
L هو طول المسار ؛
t1 - وقت بداية المسار ؛
t2 هو نهاية وقت المسار.
يتم تحديد حجم العمل ، وفقًا للمبدأ نفسه ، فقط على طول الخط الفاصل ، سيتم رسم المسافة ، وعند تنسيق حجم القوة المطبقة عند كل نقطة معينة.






